It's a Wonderful Life

source

So as I mentioned in a previous post, I'm interested in ideas about evolution and the writing of Stephen Jay Gould. I was re-reading Wonderful Life recently and I came across Gould's explanation (originally Stu Kaufman's) of the nearly incredible range of diversity in the lifeforms preserved in the Burgess Shale. The forms were so varied and unfamiliar that many appear completely unrelated to what we see today. Kauffman wanted to understand the pattern of a Cambrian explosion in species followed by decimation and evolution proceeding along only a few of the initial lines. Gould's explanation is fascinating to me, and I want to quote the entirely of it here:

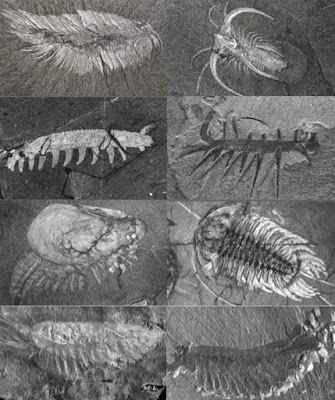
Consider the following metaphor. The earthly stage of life is a complex landscape with thousands of peaks, each a different height. The higher the peak, the greater the success -- measured as selective value, morphological complexity... of the organisms on it. Sprinkle a few beginning organisms at random onto the peaks of the landscape and allow them to multiply and to change position. Changes can be large or small, but the small shifts do not concern us here, for they only permit organisms to mount higher on their particular peak and do not produce new body plans. The opportunity for new body plans arises with rarer large jumps. We define large jumps as those that take an organism so far away from its former home that the new landscape is entirely uncorrelated with the old. Long jumps are enormously risky, but yield great reward for rare success. If you land on a peak higher than your previous home, you thrive and diversify; if you land on a lower peak or valley, you're gone.

Now we ask, how often does a large jump yield a successful outcome? Kauffman proves that the probability of success is quite high at first, but drops precipitously and soon reaches an effective zero -- just like the history of life. This pattern matches our intuitions. The first few species are placed on the landscape at random. This means that, on average, half the peaks are higher, half lower, than the initial homes. Therefore, the first long jump has a roughly 50% chance of success. But now the triumphant species stands on a higher peak -- and the percentage of still loftier peaks has decreased. After a few successful jumps, not many higher peaks remain unoccupied, and the probability of being able to move at all drops precipitously. In fact, if long jumps occur fairly often, all the high peaks will be occupied pretty early in the game, and no one has any place to go. So the victors dig in and evolve developmental systems so tied to their peaks that they couldn't change even if the opportunity arose later. Thereafter, all they can do is hang tough on their peak or die. It's a difficult world, and many meet the latter fate, not because ecology is a darwinian log packed tight with wedges, but because even random extinctions leave spaces now inaccessible to everyone. Kauffman could even quantify the precipitous decline of possibilities for successful jumps. The waiting time to the next higher peak doubles after each successful jump. (Stu told me that a mountain of athletic data shows that when a record is fractured, the average time to the next break doubles.)

Again that holy grail of nomotheticism, finding a law! The conceptual model reminds me of Holling's "basins of attraction" or Gunderson's cup and ball model of ecosystem resilience. A surface of suitability determines what outcomes are possible, although I guess it's inverted for the ecosystem model. The valleys are where conditions tend to stabilize, and peaks are just there to define the boundaries between alternative steady states.